Microstrip formulas comparison.

07 Jul 2024

Introduction

The designer has several tools and formulas available to calculate the characteristic impedance of microstrip lines. Some are highly precise but rather complex like the Hammerstad and Jensen formulas^1,2,3, while others are rather simple but with questionable accuracy like the IPC-2141 formulas^4,5,6. While approximations can be useful for the first steps of a design, their accuracy must be evaluated before use. The authors of Qucs³ made some comparison, but this comparison don’t include the common IPC formulas^5,6. A comparison of the most common microstrip calculation formulas is shown here.

While Hammerstad and Jensen formulas¹ stay the gold standard, other formulas can be safely used but that IPC-2141 formulas^4,5,6 must be used with extreme caution.

Geometry of the problem

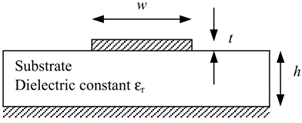
Fig. 1 – Geometry of a microstrip line⁴.

The geometrical parameters of the microstrip line studied are defined in Fig. 1⁴: w is the width of the microstrip line, h the height of the substrate, t the thickness of the strip. Non-geometrical parameters are the relative permittivity of the substrate. We’ll note for the characteristic impedance of free space.

To simplify the analysis, the strip conductivity is assumed to be infinite, the substrate losses to be null, the thickness t to be null and the frequency to be null. Note that the infinite conductivity hypothesis implies the absence of low-frequency dispersion^7,8. These assumptions are often used in RF and microwave design, and are of good accuracy for the impedance calculation.

Reference formula for Microstrip

Evaluating the accuracy of models needs a reference to compare to. Hammerstad and Jensen formulas are the most accurate closed-form formulas, and their accuracy is higher than manufacturing processes. They are commonly used in CAD software^3,9 in which the accuracy of the models of single microstrip lines without discontinuities is recognized. However, these formulas are so complex than their practical use for a comparison can lead to type errors during implementation, which can lead to inaccuracies. 3D EM simulations can be as accurate as needed, but their setup and calculation time is time consuming when accuracy is needed. Measurements are highly expensive due to the need of accuracy in both manufacturing and characterization of board materials. So, for this setup, a well-known software is used, TXLine from AWR. This software implements probably Hammerstad and Jensen formulas and its wide use almost guarantees that the implementation is bug free.

Formulas to be compared

The formulas to be compared are the following:

TXLine

TXLine is a small software, lightweight and free to use, from AWR, which allows to calculate the characteristic impedance of transmission lines like microstrip and striplines. A screenshot is shown Fig. 2.

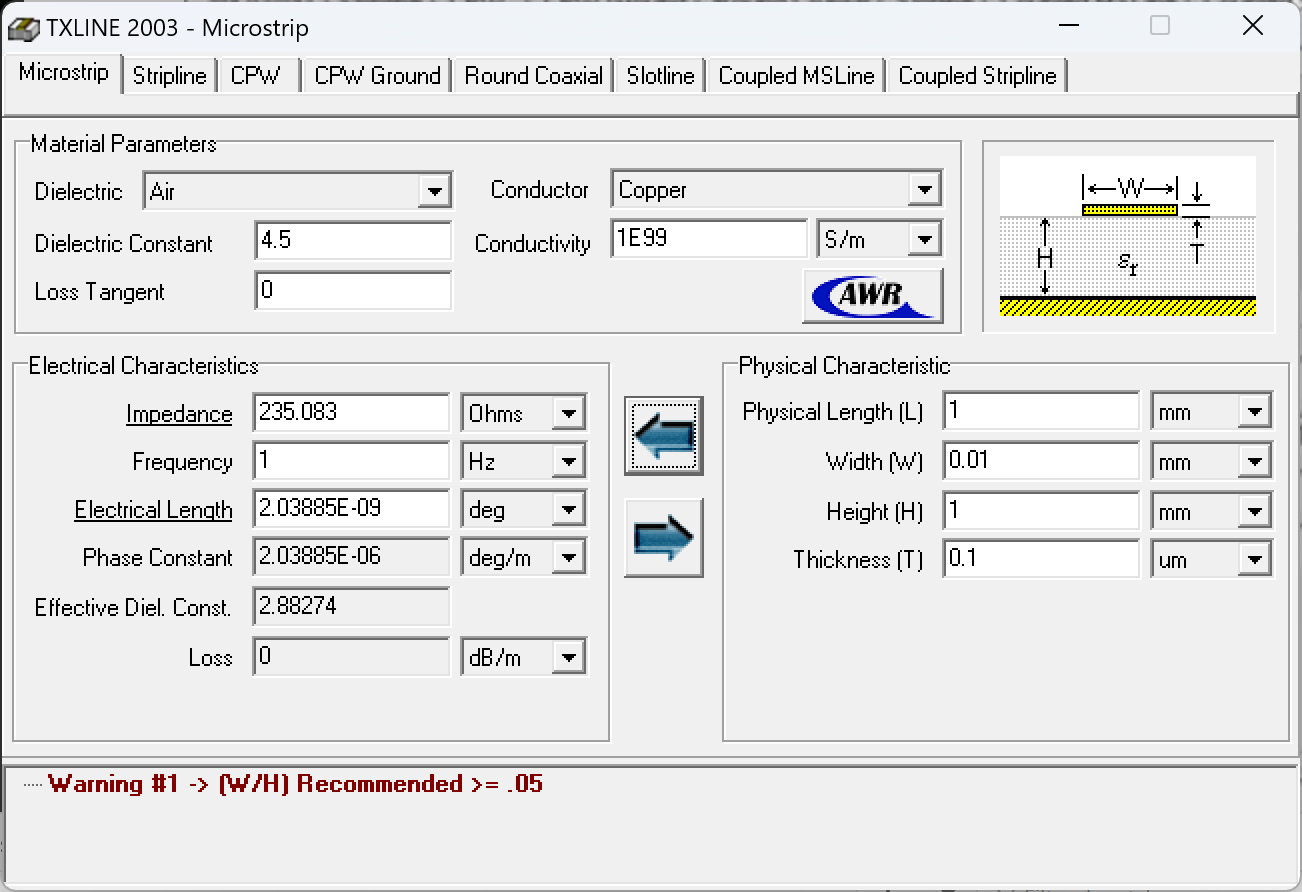
Since TXLine has no direct option to handle the infinite conductivity, the zero thickness or the zero frequency, they were approximated as follows: conductivity 10^99\ "S"\cdot"m"^-1, thickness 0.1 µm or 0.001 µm (depending on cases), and frequency 1 Hz. The high conductivity can be considered as infinite for all practical purposes, and is high enough to avoid the impact of low-frequency dispersion on the calculation results ^7,8. The thickness also is low enough to approximate the zero-thickness condition.

Hammerstad and Jensen

According to Hammerstad and Jensen formulas^1,2,3 the calculation is made in two steps. First, the effective dielectric constant is calculated:

\begin{array}{c} u(w, h) = \frac{w}{h} \\ a(u) = 1 + \frac{1}{49} \cdot \ln \left[ \frac{u^4 + \left( \frac{u}{52} \right)^2}{u^4 + 0.432} \right] + \frac{1}{18.7} \cdot \ln \left[ 1 + \left( \frac{u}{18.1} \right) \right] \\ b(\varepsilon_r) = 0.564 \cdot \left( \frac{\varepsilon_r - 0.9}{\varepsilon_r + 3} \right)^{0.053} \\\ \varepsilon_{r, \text{eff}}(u, \varepsilon_r) = \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r - 1}{2} \cdot \left( 1 + \frac{10}{u} \right)^{-a(u) \cdot b(\varepsilon_r)} \\ \end{array}

Thereafter, the following formulas are used to calculate the characteristic impedance of the microstrip line, assuming the line is in an homogeneous medium of dielectric constant :

\begin{array}{c} f(u) = 6 + (2 \cdot \pi - 6) \cdot \exp \left[ - \left( \frac{30.666}{u} \right)^{0.7528} \right] \\ Z_L(u) = \frac{Z_{F0}}{2 \cdot \pi \cdot \sqrt{\varepsilon_{r, \text{eff}}}} \cdot \ln \left[ \frac{f(u)}{u} + \sqrt{1 + \left( \frac{2}{u} \right)^2} \right] \end{array}

Note that in reference¹, the formulas are not very clear about whether or should be used, but this point was double-checked in the Excel spreadsheet formulas.

These formulas are used in these calculators^10,11.

Wheeler 1965

Wheeler’s formulas are sometimes encountered in technical literature^3,12. They are rather accurate for most uses, as will be seen in following sections. Their main problem is the undesirable impedance step. Note that, contrary to Hammerstad and Jensen formulas, the effective dielectric constant is not used in the characteristic impedance formulas.

Z_L(w, h, \varepsilon_r) = \begin{cases} \frac{Z_{F0}}{2\sqrt{\varepsilon_r}} \cdot \left( \frac{w}{2h} + \frac{1}{\pi} \cdot \ln 4 + \frac{\varepsilon_r + 1}{2\pi\varepsilon_r} \cdot \ln \left[ \frac{\pi \cdot e}{2} \cdot \left( \frac{w}{2h} + 0.94 \right) \right] + \frac{\varepsilon_r - 1}{2\pi\varepsilon_r^2} \cdot \ln \left( \frac{e \cdot \pi^2}{16} \right) \right) & \text{if} \quad \frac{w}{h} \leq 3.3 \\ \\ \frac{Z_{F0}}{\pi \sqrt{2(\varepsilon_r + 1)}} \cdot \left[ \ln \left( \frac{4h}{w} \right) + \sqrt{\left( \frac{4h}{w} \right)^2 + 2} - \frac{1}{2} \cdot \frac{\varepsilon_r - 1}{\varepsilon_r + 1} \cdot \left( \ln \frac{\pi}{2} + \frac{1}{\varepsilon_r} \cdot \ln \frac{4}{\pi} \right) \right] & \text{if} \quad \frac{w}{h} > 3.3 \end{cases}

We have not found any calculator using these formulas.

Wheeler 1977

Wheeler 1977 formulas are seen more often than Wheeler 1965 formulas in literature^4,13,14,15. They are attributed sometimes to Wadell because he made a good summary in his book¹³. Note that these formulas are incorrectly typed a reference⁴, where a pi^2 was incorrectly replaced by a sqrt(pi), and an extra square root is present, as pointed by an other reference¹⁶.

\begin{array}{c} A = \frac{14 + \frac{8}{\varepsilon_r} \cdot \frac{4 \cdot h}{w'}}{11} \\ B = \sqrt{A^2 + \frac{1 + \frac{1}{\varepsilon_r} \cdot \pi^2}{2}} \\ Z_L = \frac{Z_{0F}}{2 \cdot \sqrt{2} \cdot \pi \cdot \sqrt{\varepsilon_r + 1}} \cdot \ln \left[ 1 + \frac{4 \cdot h}{w} \cdot (A + B) \right] \end{array}

They are used in several microwave calculators^{17,18,19,20,21}. Calculator²¹ has a mistake in the handling of epsilon_(r,"eff"), which can be diagnosed by calculating impedances with epsilon_r=1.

No explicit formula is given for epsilon_(r,"eff"). The reason is that it can be calculated with: epsilon_(r,"eff")=[(Z_0(h,w,epsilon_r=1))/(Z_0(h,w,epsilon_r=epsilon_r))]^2. This makes these formulas both simple and complex at the same time. In a programming language, it is easy to define a function and to use it two times to calculate . In an old school Excel sheet this would lead to use twice plus one many columns, which more than Hammerstad & Jansen formulas.

Hammerstad 1975 formulas

Often seen in websites²² or in lectures on microwave techniques^23,24, Hammerstad’s 1975 formulas are the following^{22,25,26,27,28}. They are often attributed to Bahl, who made an improvement to their strip thickness correction^26,27, not investigated in this article, but the zero-thickness formulas originates from Hammerstad²⁵.

\begin{eqnarray} \varepsilon_{r, \text{eff}} &=& \begin{cases} \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r - 1}{2} \cdot \left( \left(1 + \frac{12 \cdot h}{w}\right)^{-1/2} + 0.04 \cdot \left(1 - \frac{w}{h}\right)^2 \right) & \text{if} \quad \frac{w}{h} \leq 1 \\ \\ \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r - 1}{2} \cdot \left( 1 + \frac{12 \cdot h}{w} \right)^{-1/2} & \text{if} \quad \frac{w}{h} > 1 \end{cases} \\ Z_L &=& \begin{cases} \frac{Z_0}{2 \cdot \pi \cdot \sqrt{\varepsilon_{r, \text{eff}}}} \cdot \ln \left( \frac{8 \cdot h}{w} + \frac{w}{4 \cdot h} \right) & \text{if} \quad \frac{w}{h} \leq 1 \\ \\ \frac{Z_{F0}}{\sqrt{\varepsilon_{r, \text{eff}}}} \cdot \left[ \frac{w}{h} + 1.393 + 0.667 \cdot \ln \left( \frac{w}{h} + 1.444 \right) \right]^{-1} & \text{if} \quad \frac{w}{h} \geq 1 \end{cases} \end{eqnarray}

These formulas are used in these calculators^29,30,31. Note that this calculator³⁰ also includes frequency thickness correction and dispersion.

Schneider

Not often seen, Schneider formulas^3,32 are as following:

\varepsilon_{r, \text{eff}} = \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r - 1}{2} \cdot \frac{1}{\sqrt{1 + 10 \cdot \frac{h}{w}}} Z_L = \frac{Z_{F0}}{\sqrt{\varepsilon_{r, \text{eff}}}} \cdot \begin{cases} \frac{1}{2 \cdot \pi} \cdot \ln \left( \frac{8 \cdot h}{w} + \frac{w}{4 \cdot h} \right) & \text{if} \quad \frac{w}{h} \leq 1 \\ \\ \frac{1}{\frac{w}{h} + 2.42 - 0.44 \cdot \frac{h}{w} + \left(1 - \frac{h}{w}\right)^6} & \text{if} \quad \frac{w}{h} > 1 \end{cases}

We have not found any calculator using this formula.

IPC-2141 formulas

The IPC-2141 formulas^4,5,6,28 are very popular. However, despite their popularity, they should be used with extreme caution, as will be demonstrated during our comparison, because their range of validity is extremely narrow, and they have a bad asymptotic behavior.

Although they are widely quoted, their narrow range of validity is much less often quoted²⁸: 0.1<w/h<2.0 and 1<epsilon_r<15. This range becomes even narrower because it enables to synthesize 50 Ω lines only for 3.9<epsilon_r<15.

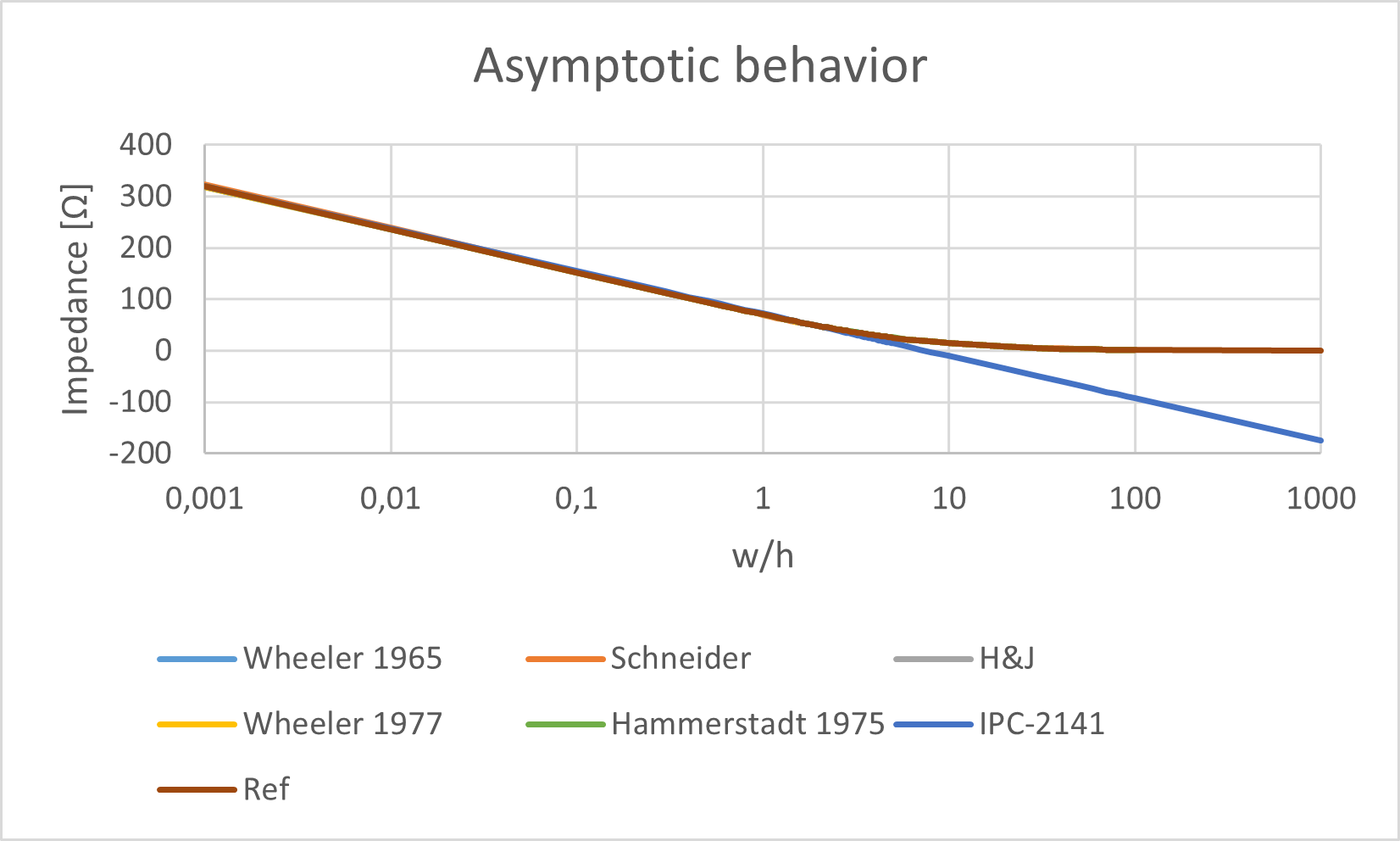
Contrary to other formulas (Hammerstad and Jensen, Wheeler 1965, Wheeler 1977, Schneider and Hammerstad 1975), IPC-2141 formulas have a totally nonsense asymptotic behavior. All other formulas were found to have an accuracy better than 1.5 % for epsilon_r=4.5 and w/h ratios ranging from 0.001 to 1000. On the contrary, IPC-2141 formulas give a nonsense negative impedance result for w/h>7.5. This is a large line for most applications, but it still happens in some designs, and give an idea of the problem.

Fig. 1 compares the asymptotic behavior of IPC-2141 formulas with the good formulas. While IPC-2141 have a very bad asymptotic behavior for large lines, all good formulas have a good asymptotic behavior on the very wide range 0.001<w/h<1000, well outside of their guaranteed validity range.

Despite the problems of IPC-2141 formulas, they are used in several online calculators^{33,34,35,36,37,38,39,40}. Some calculators^33,34,35 give warnings when using IPC-2141 formulas outside of their validity range like shown in Fig. 3. On the contrary, some other calculators^{36,37,38,39,40} give neither a warning nor a validity range, including a calculator on a renowned website³⁸. Worse, some calculators^38,39,40 even give nonsense negative impedance when fed with proper values without any warning.

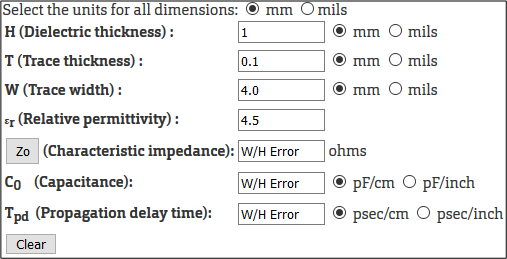
Fig. 4 – Screenshot of a microstrip line impedance calculator³³ raising a warning when trying to calculate impedances outside IPC-2141 validity range.

It should be mentioned that a calculator³³ not only gives the validity range of the IPC-2141 formula and warns when trying to enter parameters outside of this range, but it also gives accuracy data.

Comparison results

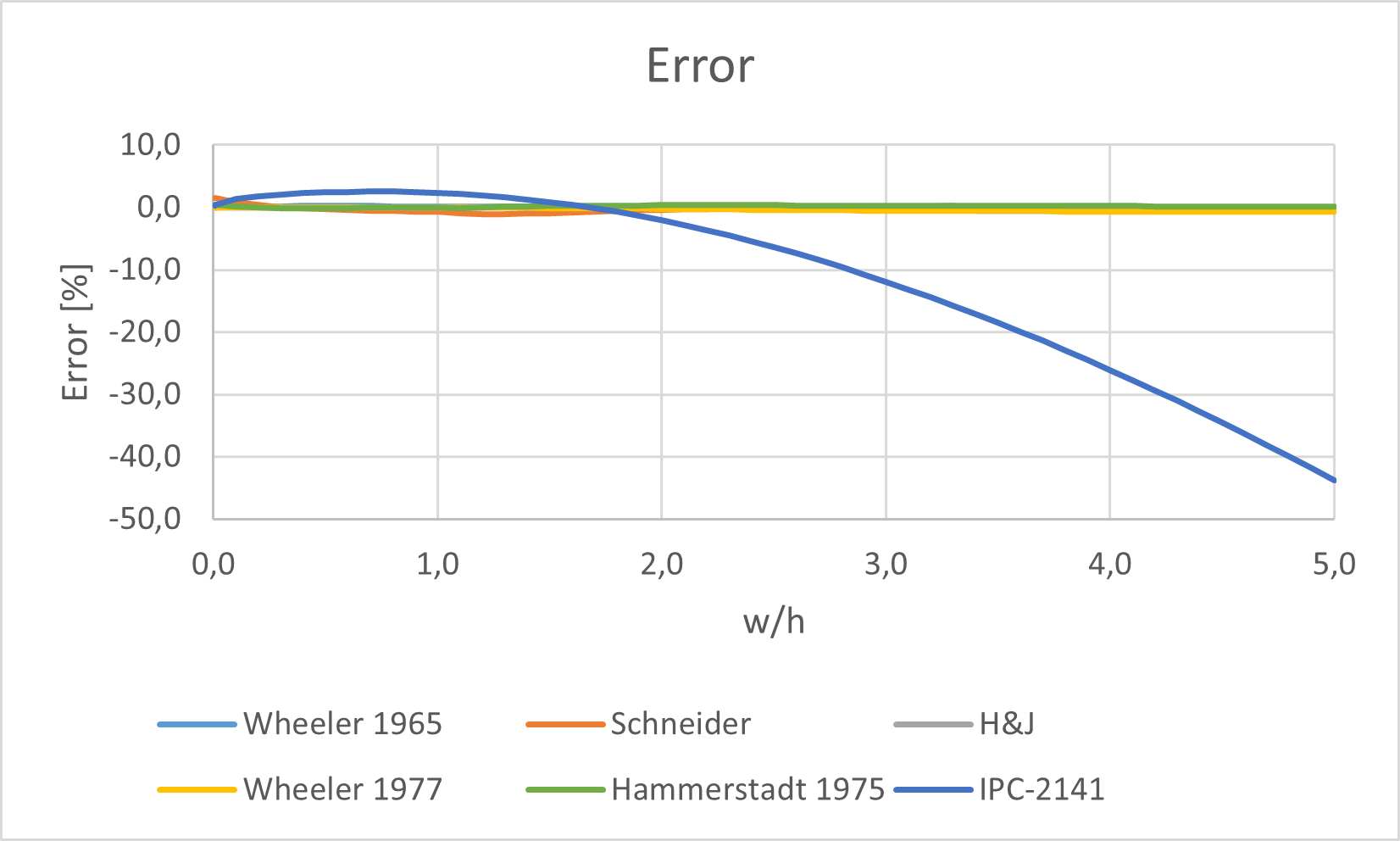
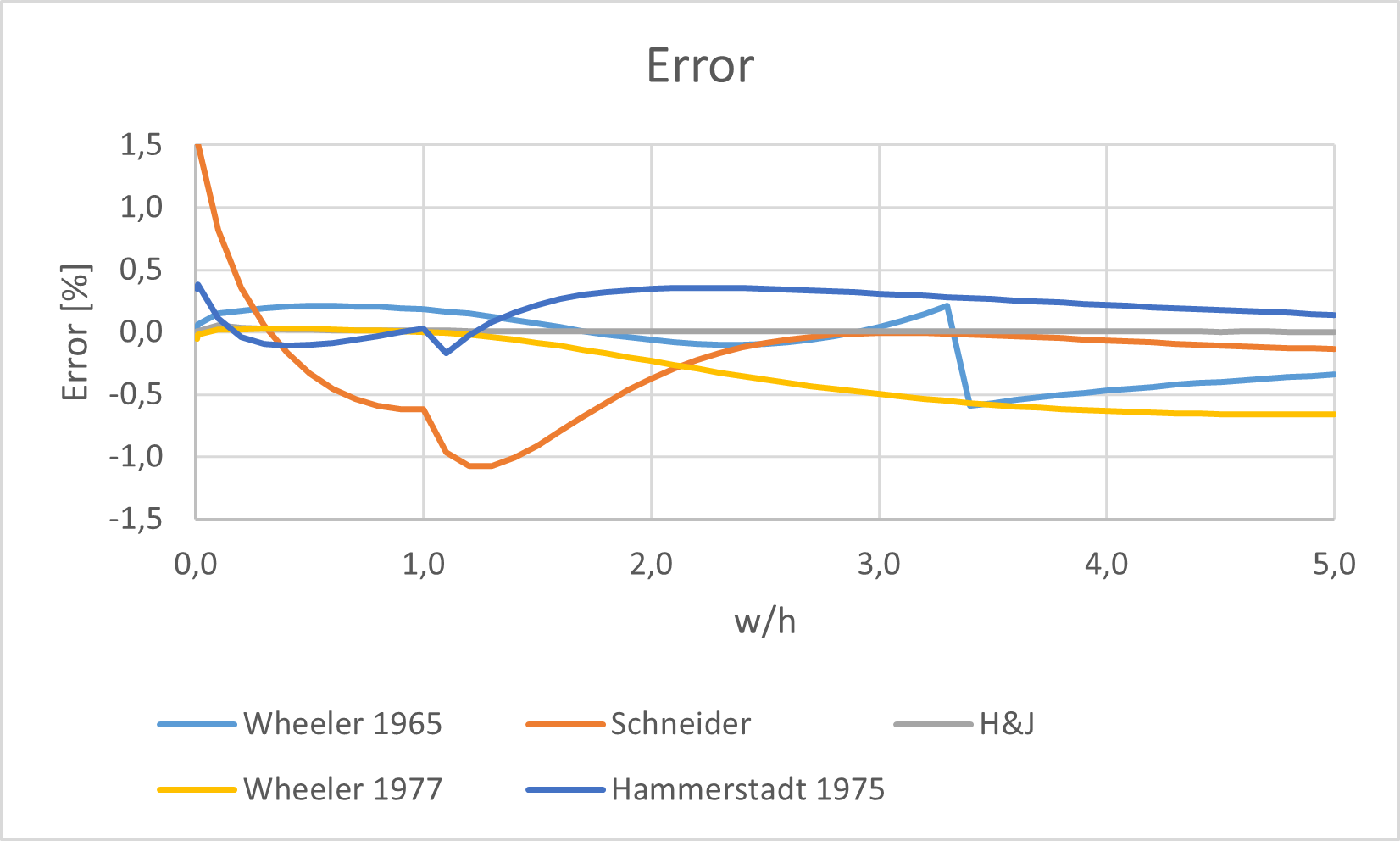
From the Fig. 5 graph, a clear outsider in inaccuracy is the IPC-2141 formula, reaching up to 44 % inaccuracy! This formula will be commented later. Fig. 6 graph, without the IPC-2141 formula on a reduced scale, shows the relative error of the remaining formulas.

The H&J formulas are probably the formulas used in TXLine software since the calculated difference between them is lesser than 0.06 % ! Note that this calculated error is always positive, because TXLine took a line thickness which is non-zero, although very thin, contrary to our calculation. Since we are comparing the H&J formulas to themselves, this benchmark does not prove that they are the most accurate. However, since they are believed to be the most accurate in all the recent literature, we’ll stick to that conclusion. They still have the inconvenient of their complexity, which can lead to potential typing mistakes.

Hammerstad 1975 formulas are at the second place for accuracy: error less than 0,38 % on tested values. However, they still have the inconvenience of their complexity, potentially leading to typing mistake, and of the different expressions for different subdomains.

Wheeler 1965 formulas are at the third place for accuracy: error less than 0.59 % on tested values. However, the calculation step makes them troublesome to use in some cases. And, for use in Excel spreadsheets, it makes mandatory to duplicate the formulas. The 0,06 % accuracy gained from Wheeler 1977 is not worth it.

Wheeler 1977 formulas, although not very known, are rather simple and rather accurate: the error is lesser than 0.66 % on tested values. The absence of impedance steps in these formulas make them interesting.

Schneider formulas are less complex than Hammerstad 1975 formulas but less accurate. Their error is less than 1.6 %. Their interest is mainly historical.

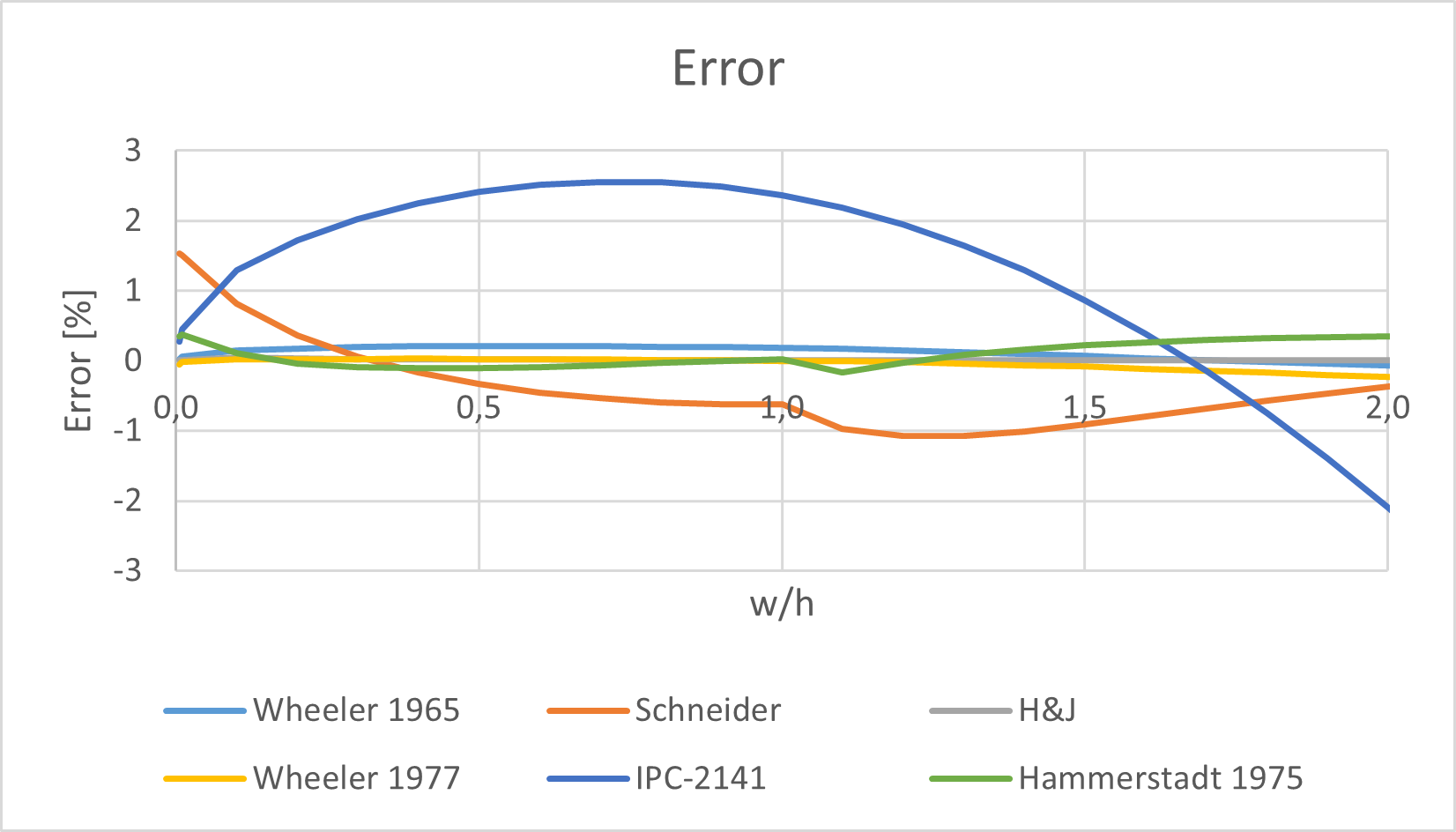
The real strange point is the accuracy of the IPC-2141 formulas. Their relative error reach 44 % on the tested values! A closer look reveals that most of the error happens when the normalized width u is higher than 2. When plotted on a narrower range, like in Fig. 7, the relative error is much lower: less than 2.1 %. This is precisely the range of values of the 50 Ω lines.

Review of calculators

The following table sums up some microstrip calculators and the formulas which they use. Only microstrip calculators for which the formula was told or could be inferred from JavaScript source code were included.

Website	Formula	Val. warn	Comments
www.microwaves101.com10	H&J
mcalc.sourceforge.net11	H&J
www.eeweb.com17	Wheeler 1977
cepd.com18	Wheeler 1977
www.finetune.co.jp19	Wheeler 1977
leleivre.com20	Wheeler 1977
chemandy.com21	Wheeler 1977		Confusion between εr and εr,eff.
www.pasternack.com29	Hammerstad 1975
www.emclab.cei.uec.ac.jp30	Hammerstad 1975
chemandy.com31	Hammerstad 1975
emclab.mst.edu33	IPC-2141	Yes
referencedesigner.com34	IPC-2121	Yes	Formulas not told in document, but seen in JavaScript source code.
technick.net35	IPC-2141	Yes
a8blog.com36	IPC-2141	No	No warnings, but at least does not print the calculated negative impedance.
www.ee.ucl.ac.uk37	IPC-2141	No	No warnings, but at least does not print the calculated negative impedance.
www.everythingrf.com38	IPC-2141	No
chemandy.com39	IPC-2141	No
ncalculators.com40	IPC-2121	No

Conclusion

While H&J formulas are the gold standard for calculations, several other formulas give a good trade-off between accuracy and simplicity which are sufficient for most applications. Wheeler 1977 is the clear winner of this tradeoff with 0.66 % error when epsilon_(r,"eff") is not needed. However, on old school Excel sheets, when epsilon_(r,"eff") is needed, the need to duplicate the calculation makes it not anymore convenient than H&J formulas. In this case, Hammerstad 1975 is the winner of this tradeoff with 0.38 % error.

IPC-2141 formulas have severe issues and must be used with extreme caution.