F4INX corner

Hadrien F4INX's blog: radiofrequency electronics, EM simulations, ....

© 2026 Hadrien Theveneau. See licence.

https://f4inx.github.io/posts/backoff.html

Backoff calculations.

22 Dec 2025

Many thanks to my management at Eutelsat who kindly allowed me to republish this document I wrote for internal use here. Many thanks to my fellow colleagues for their help in this document.

Introduction

Power amplifiers have a limit on the maximum power they can amplity while staying linear, that is, keeping distorsion low enough.

For sinusoidal signals, it is straightforward to keep the power of the signal below the maximum linear power. However, for multi-carrier signals, the signal has peaks much higher than its average power, and keeping these paks below the maximum linear power requires to have a maximum power much higher than the average power, which is costly and inefficient in power.

Since these peaks are rare, it is possible to accept that some peaks go beyond the maximum linear power, provided that the resulting distorsion is acceptable. This allow to reduce the difference between the average power and the maximum power of the amplifier.

The needed difference between the average power and the maximum power, called backoff, is not straightforward to calculate for multi-carrier signals. This article proposes an investigation of this topic and guidelines to estimate the needed backoff.

The multi-carrier signal occurs either due to multi-carrier modulation schemes or when an amplifier serves multiple users.

Existing rules of thumb do not provide a precise method to make a compromise between an high backoff, which wastes power, and a low backoff, which may not provide enough linearity. The peak to average power ratio (PAPR) is insufficient since it does not indicate how often peak levels are reached.

Modelling

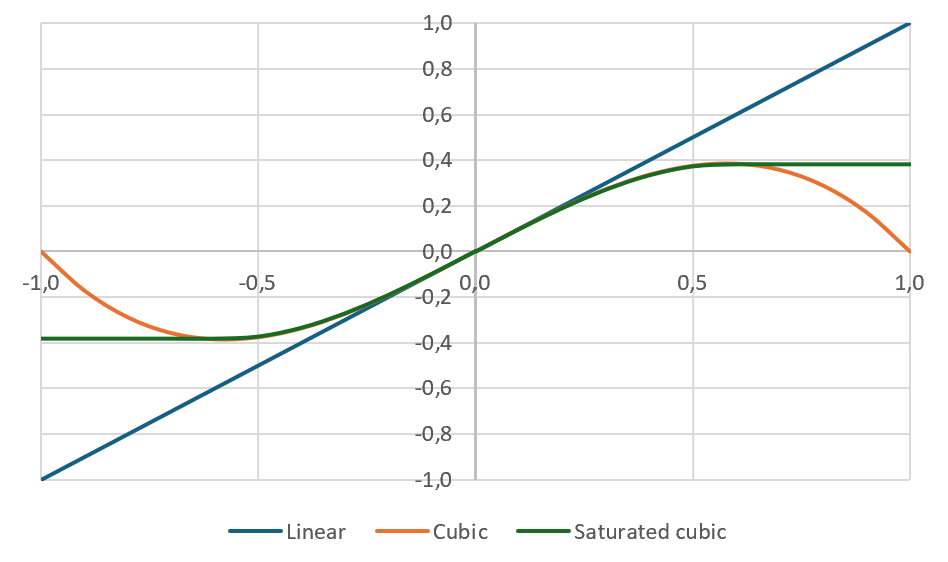
An ideal amplifier has a linear transfer function in an infinite range.

Real amplifiers have a limited linear range and their transfer function is closer to the saturated cubic model of following curve.

This saturated cubic function is hard to model so the cubic model, valid for signals lower than saturation of the amplifier, is used instead. This is the domain of most often used in telecommunications.

This cubic transfer function can be expressed by the following equation:

y = x - \alpha \cdot \left|x\right|^2 \cdot x

Signals are modelled as a complex amplitude at amplifiers centre frequency.

This approach is based on the works of Roblin and Versprecht.

The following assumptions are made:

  • Nonlinear effects are modelled as an amplitude transfer function (without phase effects, without memory effects).
  • Even-order terms are ignored since they produce out-of-band distortion.
  • Higher-order odd terms are considered negligible compared to third-order terms.
  • Conjugate terms correspond to reverse spectrum output signals, which are eliminated through filtering.
  • Gain is normalized to unity because all variables of interest are normalized to output (OIP3, Psat, …).
  • Units and impedances are ignored: \text{power}=\left|x\right|^2. No \sqrt{2} is present in the power formula because complex sinusoids are considered instead of real sinusoids.

Parameters in function of OIP3

An input signal x consisting of two equal-amplitude complex sinusoids at angular frequencies ω_1 and ω_2 is considered:

x = A \cdot \left( e^{j \cdot \omega_1 \cdot t} + e^{j \cdot \omega_2 \cdot t} \right)

where A is the amplitude of each sinusoid.

To compute the tones produced by the transfer function:

y = x + \alpha \cdot \left|x\right|^2 \cdot x

The first step is to compute \left|x\right|^2:

\begin{align*} \left|x\right|^2 &= A \cdot \left( e^{j \cdot \omega_1 \cdot t} + e^{j \cdot \omega_2 \cdot t} \right) \cdot A \cdot \left( e^{-j \cdot \omega_1 \cdot t} + e^{-j \cdot \omega_2 \cdot t} \right) \\ &= A^2 \left[ 2 + e^{j \cdot \left( \omega_1 - \omega_2 \right) \cdot t} + e^{j \cdot \left( \omega_2 - \omega_1 \right) \cdot t} \right] \end{align*}

The second step is to expand the non-linear term α \cdot \left|x\right|^2 \cdot x

: \begin{align*} & \alpha \cdot \left|x\right|^2 \cdot x = \alpha \cdot A^2 \left[ 2 + e^{j \cdot \left( \omega_1 - \omega_2 \right) \cdot t} + e^{j \cdot \left( \omega_2 - \omega_1 \right) \cdot t} \right] \cdot A \cdot \left( e^{j \cdot \omega_1 \cdot t} + e^{j \cdot \omega_2 \cdot t} \right) \\ & \qquad = \alpha \cdot A^3 \cdot \left[ 2 \cdot e^{j \cdot \omega_1 \cdot t} + 2 \cdot e^{j \cdot \omega_2 \cdot t} + e^{j \cdot \left(2 \cdot \omega_1 - \omega_2\right) \cdot t} + e^{j \cdot \omega_2 \cdot t} + e^{j \cdot \omega_1 \cdot t} + e^{j \cdot \left(\omega_1 - 2 \cdot \omega_2\right) \cdot t} \right] \\ & \qquad = \alpha \cdot A^3 \cdot \left[ 3 \cdot e^{j \cdot \omega_1 \cdot t} + 3 \cdot e^{j \cdot \omega_2 \cdot t} + e^{j \cdot \left(2 \cdot \omega_1 - \omega_2\right) \cdot t} + e^{j \cdot \left(\omega_1 - 2 \cdot \omega_2\right) \cdot t} \right] \end{align*}

The total output can be split into fundamental and intermodulation components.

The total fundamental part is:

y_\text{fund} = A \cdot \left( 1 + 3 \cdot \alpha \cdot A \right) \cdot \left( e^{j \cdot \omega_1 \cdot t} + e^{j \cdot \omega_2 \cdot t} \right)

Its amplitude is changed by the non-linear effects. However, from the OIP3 definition, only the linear part should be taken.

The total linear part is:

y_\text{lin} = A \cdot \left( e^{j \cdot \omega_1 \cdot t} + e^{j \cdot \omega_2 \cdot t} \right)

and its RMS amplitude is:

y_\text{lin} = A \cdot \sqrt{2}

The total intermodulation part is:

y_\text{imd3} = \alpha \cdot A^3 \cdot \left[ e^{j \cdot \left(2 \cdot \omega_1 - \omega_2\right) \cdot t} + e^{j \cdot \left(\omega_1 - 2 \cdot \omega_2\right) \cdot t} \right]

and its RMS amplitude is:

y_\text{imd3} = \alpha \cdot A^3 \cdot \sqrt{2}

The \text{OIP3} is the (theoretical) amplitude A_\text{OIP3} where A_\text{lin}=A_\text{imd3}, i.e:

A_\text{OIP3} \cdot \sqrt{2} = \alpha \cdot A^3 \cdot \sqrt{2}

thus:

\alpha = \frac{1}{A_\text{OIP3}^2}

Non-linear power for a gaussian input

A multi-carrier signal, at both input and output, which may or may not be at the same frequency, is modelled by its complex amplitude centred on the device’s centre frequency:

\begin{gather*} x_\text{mod}(t) = \text{Re}\left[x(t) \cdot e^{j \cdot \omega_c \cdot t}\right] \\ x(t) = x_1(t) + ... + x_n(t) \\ x(t) = a_1(t) \cdot e^{j \cdot \omega_1 \cdot t} + ... + a_n(t) \cdot e^{j \cdot \omega_n \cdot t} \\ \end{gather*}

The complex amplitudes x_i(t) contains not only the base complex amplitudes of the signals a_i(t) but also the frequency shift \omega_i-\omega_c of each signal relative to the device’s centre frequency. a_i(t) can be modelled as a complex random variable without rotational symmetry. However, due to the frequency shift, x_i(t) can be modelled as a complex random variable with rotational symmetry.

The sum of the complex amplitudes x(t)=x_1 (t)+...+x_n(t) can be approximated by a zero-mean Gaussian probability distribution with a variance corresponding to its power. The following curve1, for a rolling dice, shows that starting from 3 rolls, the curve is close enough to gaussian.

To simplify calculations, the input/output power is normalized to 1, so:

\sigma=\sqrt{\text{power}} = 1

  1. https://commons.wikimedia.org/wiki/File:Somme_n_tirages_pile_ou_face_1_a_12.svg ↩

Power of linear component

The linear part of the output is:

y_\text{lin} = x

which has a power of:

\text{E}\left[\left|y_\text{lin}\right|^2\right] = \text{E}\left[\left|x\right|^2\right] = \sigma^2 = 1

which is consistent with our normalization hypothesis.

Power of non-linear component

The non-linear part of the output (including change in fundamental) is given by:

y_\text{NL} = \alpha \cdot \left|x\right|^2 \cdot x

whose power is:

\text{E}\left[\left|y_\text{NL}\right|^2\right] = 6 \cdot \left|\alpha\right|^2

It can be calculated as follows:

\begin{gather*} \left|y_\text{NL}\right|^2 = \left|\alpha \cdot \left|x\right|^2 \cdot x\right|^2 = \alpha^2 \cdot \left|x\right|^6 \\ \text{E}\left[\left|y_\text{NL}\right|^2\right] = \left|\alpha\right|^2 \cdot \text{E}\left[\left|x\right|^6\right] \\ \text{E}\left[\left|x\right|^6\right] = \text{E}\left[s^3\right] \quad \text{with} \quad s = \left|x\right|^2 \end{gather*}

The total power of x is normalized to 1 so the power of its real and imaginary components are both \frac{1}{2}. In mathematical terms, x follows a standard complex normal distribution, so \text{Re}[x] and \text{Im}[x] both follow2 a normal distribution of variance \frac{1}{2}. Consequently, 2 \cdot s follows a Chi-squared probability distribution3 with two degrees of freedom, itself equal to an exponential distribution of parameter \frac{1}{2}, whose moments can be calculated as such4:

\begin{gather*} 2 \cdot s \sim \chi_2^2 = \text{Exp}\left[\frac{1}{2}\right] \\ \text{E}\left[\left(2 \cdot s\right)^3\right] = \frac{3!}{\left(\frac{1}{2}\right)^2} = 3! \cdot 2^3 = 48 \\ \text{E}\left[s^3\right] = \frac{48}{2^3} = 6 \end{gather*} Hence: \text{E}\left[\left|y_\text{NL}\right|^2\right] = 6 \cdot \left|\alpha\right|^2

  1. https://en.wikipedia.org/wiki/Complex_normal_distribution ↩

  2. https://en.wikipedia.org/wiki/Chi-squared_distribution ↩

  3. https://en.wikipedia.org/wiki/Exponential_distribution ↩

Power of the non-linear component in function of the OIP3 and the backoff

The ratio P_\text{NL,dBc} between the power of the non-linear perturbation and the wanted signal is:

P_\text{NL,dBc} = 10 \cdot \log_{10}\left(6\right) + 2 \cdot (P_\text{out,dBm} - \text{OIP3}_\text{dBm})

This can be calculated as follows by combining the previous results:

P_\text{NL} = 6 \cdot \left|\alpha\right|^2 = 6 \cdot \frac{1}{A_\text{OIP3}^4}

which can be expressed in dBc since the output power is normalized to unity:

\begin{align*} P_\text{NL,dBc} &= 10 \cdot \log_{10}\left(6\right) - 40 \cdot \log_{10}\left(A_\text{OIP3}\right) \\ &= 10 \cdot \log_{10}\left(6\right) - 2 \cdot \text{OIP3}_\text{dBc} \end{align*}

and expressing the OIP3 in dBm:

P_\text{NL,dBc} = 10 \cdot \log_{10}\left(6\right) + 2 \cdot (P_\text{out,dBm} - \text{OIP3}_\text{dBm})

From this, the maximum ouput power for a given P_\text{NL,dBc} can be calculated as:

P_\text{out,dBm} = \text{OIP3}_\text{dBm} - \frac{10 \cdot \log_{10}\left(6\right)}{2} - \frac{1}{2} \cdot \left| P_\text{NL,dBc} \right|

with the absolute value to get rid of the sign issues in P_\text{NL,dBc}, mathematically negative but often expressed without sign.

In telecommunications, the maximum power is more often used than the \text{OIP3}:

P_\text{out,dBm} = P_\text{sat,dBm} + \left(\text{OIP3}_\text{dBm} - P_\text{sat,dBm}\right) - \frac{10 \cdot \log_{10}\left(6\right)}{2} - \frac{1}{2} \cdot \left| P_\text{NL,dBc} \right|

The quantity \text{OIP3}_\text{dBm} - P_\text{sat,dBm} will be called in the following \text{LF} for linearity factor because it it higher when the amplifier is more linear. Estimations of this quantity will be given in the following sections.

The quantity P_\text{sat,dBm} - P_\text{out,dBm} is called the \text{OBO} for output backoff and can be expressed as:

\text{OBO} = -\text{LF} + \frac{10 \cdot \log_{10}\left(6\right)}{2} + \frac{1}{2} \cdot \left| P_\text{NL,dBc} \right|

Values of the linearity factor LF for different technologies

The previous equations for the calculation need \text{LF} =\text{OIP3}_\text{dBm} - P_\text{sat,dBm}. To have estimates of its value, a review of several typical amplifiers was performed.

TWTA

LF between 4 and 6.

Mfg.NameDescriptionPsat [W]Psat [dBm]IM [dBc]IM value at [dBm]OIP3 [dBm]OIP3 - Psat [dB]
CPIT04UO-A1400 W CW TWTA40056,0-24,049,061,05,00
CPITL07UO 750 W SuperLinear® TWTA5 75058,8-24,051,263,24,45
CPIT07UO 750 W CW TWTA6 75058,8-24,051,163,14,35
CPITL12UO-A1 1.25 kW SuperLinear® TWTA (Air Cooled)7 125061,0-25,054,366,85,84
CPITL12UO-L11.25 kW SuperLinear® TWTA (Liquid Cooled)125061,0-25,054,366,85,84

  1. https://www.cpii.com/docs/datasheets/817/tl07uo_mkt327.pdf ↩

  2. https://www.cpii.com/docs/datasheets/817/MKT-285%202024%20rev%20V.pdf ↩

  3. https://www.cpii.com/docs/datasheets/817/tl12uo-a1_mkt257.pdf ↩

TWTA with linearizer

Same products as before but with linearizer option. LF between 8 and 9.

Mfg.NameDescriptionPsat [W]Psat [dBm]IM [dBc]IM value at [dBm]OIP3 [dBm]OIP3 - Psat [dB]
CPIT04UO-A1400 W CW TWTA40056,0-24,052,064,08,00
CPITL07UO750 W SuperLinear® TWTA75058,8-25,055,267,78,95
CPIT07UO750 W CW TWTA75058,8-26,054,167,18,35
CPITL12UO-A11.25 kW SuperLinear® TWTA (Air Cooled)125061,0-25,057,369,88,85
CPITL12UO-L11.25 kW SuperLinear® TWTA (Liquid Cooled)125061,0-25,057,369,88,85

SSPA

LF between 8 and 10.

Mfg.NamePsat [W]Psat [dBm]IM [dBc]IM value at [dBm]OIP3 [dBm]OIP3 - Psat [dB]
SpacePath STS168 2043,0-25,039,051,58,5
SpacePath ST209 2544,0-25,040,052,58,5
SpacePath ST25K10 3245,0-25,041,053,58,5
SpacePath STS25011 25154,0-25,051,063,59,5
SpacePath STS30012 31655,0-25,052,064,59,5
SpacePath STS40013 39856,0-25,053,065,59,5
SpacePath STS50014 50157,0-25,054,066,59,5
Advantech SapphireBlu15 100060,0-25,056,569,09,0

  1. https://www.space-path.com/sites/default/files/document-downloads/Datasheet%2016%2020%2025W%20Ku%20Band.pdf ↩

  2. https://www.space-path.com/sites/default/files/document-downloads/Datasheet%2016%2020%2025W%20Ku%20Band.pdf ↩

  3. https://www.space-path.com/sites/default/files/document-downloads/Datasheet%2016%2020%2025W%20Ku%20Band.pdf ↩

  4. https://www.space-path.com/sites/default/files/document-downloads/STS250%20300%20400%20500%20K.pdf ↩

  5. https://www.space-path.com/sites/default/files/document-downloads/STS250%20300%20400%20500%20K.pdf ↩

  6. https://www.space-path.com/sites/default/files/document-downloads/STS250%20300%20400%20500%20K.pdf ↩

  7. https://www.space-path.com/sites/default/files/document-downloads/STS250%20300%20400%20500%20K.pdf ↩

  8. https://advantechwireless.com/wp-content/uploads/2022/11/PB-SAPPH-2G-Ku-1000W-22245-LM.pdf ↩

SSPA with dubious linearization

To be continued. The example found has a surprisingly low LF.

Mfg.NamePsat [W]Psat [dBm]IM [dBc]IM value at [dBm]OIP3 [dBm]OIP3 - Psat [dB]
Teledyne HPAK2600AHXXXXXG16 60057,8-2554,867,39,5

  1. http://www.satcomsource.com/Teledyne-Paradise-Datacom-400W-Outdoor-Ku-Band-GAN-SSPA.pdf ↩

Calculated values of backoff for - 20 dBc

The value of LF depends on the technology but is surprisingly constant inside a given technology. It is this possible to calculate recommended backoff values for each technology.

TechnologyLF minBack-off
TWTA49,9
TWTA with linearizer85,9
SSPA85,9

Related posts