Hilbert transform demo.

21 Dec 2025

The discrete Hilbert transform seems rather mysterious. However, the principle as well as his mathematics are not so complicated: the Hilbert transform is mainly a way to add a 90° phase shift to a signal and its equation can be explained from simple mathematical principles and an Excel spreadshet.

Pulse

The first step is to start with a discrete unit pulse sampled using 11 points: the center point at 1 and the others at 0. For parity reasons, only 6 sinus are needed in the discrete Fourier transform.

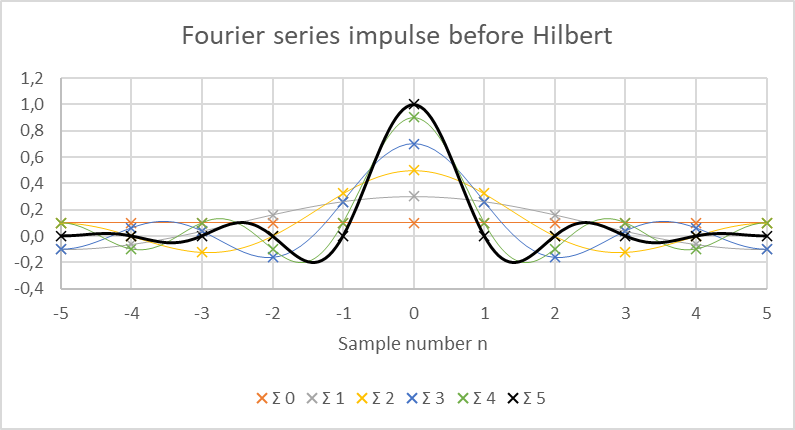
Note that in the equation, not only the discrete points are calculated, but also the points in between to have curve easier to visualise. This smoothing is similar to a reconstruction filter.

Transformed pulse

The next step is to apply a 90° phase shift to all the sinusoids of the previous sum.

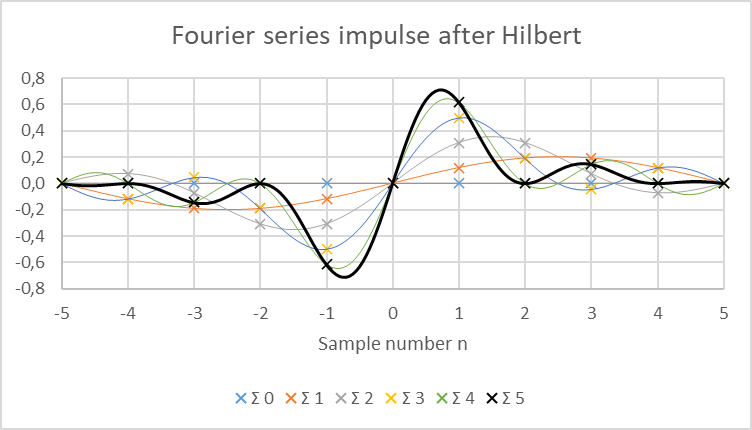
The resulting sum gives the Hilbert transform of the starting pulse. It is compared to the mathematical equation of the discrete Hilbert transform of a pulse for a finite number of samples in the following plot. Note that the red line gives the value of the transform only for the odd points, the others being at 0.

\begin{equation} h[n] = \left\{\begin{array}{cl} 0 & \text{if} \; n \; \text{even} \\ \frac{2}{N \cdot \tan\left(\pi \cdot \frac{n}{N}\right)} & \text{if} \; n \; \text{odd} \end{array}\right. \end{equation}

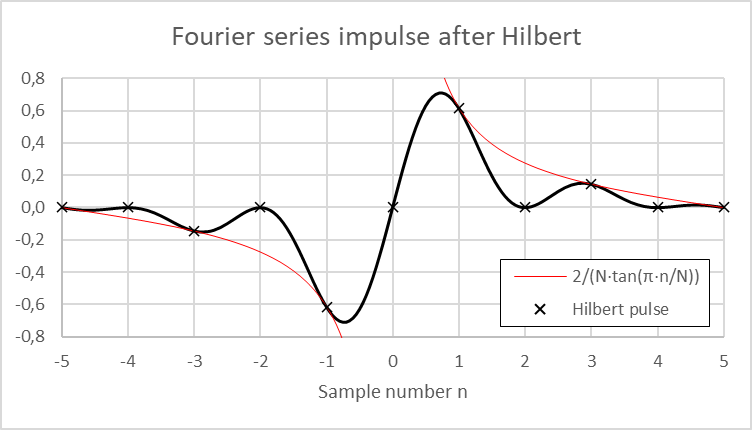
Infinite number of samples

This demonstration was performed using a finite number of samples, rather small. In real cases, the number of samples is likely to be infinite, either as an approximation or a big number of samples or as a continuous flow like in software defined radio (SDR). The question of the practical implementation of these cases is left aside. For an infinite number of samples, the limit can be calculated as follows:

\begin{align*} &\tan\left(x\right) \sim x \\ &\tan\left(\pi \cdot \frac{n}{N}\right) \sim \pi \cdot \frac{n}{N} \\ &\frac{2}{N \cdot \tan\left(\pi \cdot \frac{n}{N}\right)} \sim \frac{2}{N \cdot \pi \cdot \frac{n}{N}} = \frac{2}{\pi \cdot n} \end{align*}

which is the usual result.

Excel files to download

• Hilbert transform demo [French]: Hilbert-demo.xlsx.
• Hilbert transform demo [English]: Hilbert-demo-EN.xlsx.